Fundamentally, broadcasting is the technique of creating arrays of various forms fit for element-wise operations. Imagine two arrays you wish to combine—one larger and one smaller. Broadcasting automatically shapes the smaller array in a way that lets the operation run naturally instead of shrinking the smaller array to fit the dimensions of the larger one.
Boardcast function similar function “stretches” the smaller array across the larger one by copying its values essentially. This makes element-wise additions, multiplies, and more possible without explicitly looping or scaling.
Importance of Broadcasting in Programming
In the fields of data science, machine learning, and deep learning especially broadcasting is quite important. Many times dealing with multidimensional arrays (tensors), these disciplines can find manual operations on them difficult. By use of broadcasting, these activities become simpler and more understandable, freeing developers to concentrate on the program’s real logic.
Furthermore, especially in relation to big datasets, broadcasting greatly accelerates activities. One would have to create long codes or manually change data structures to make them compatible for mathematical operations without broadcasting. That process is automated via broadcasting, so saving time and labor.
How Broadcasting Works
Broadcasting works by following a set of rules. These rules ensure that the shapes of the arrays are compatible for operations:
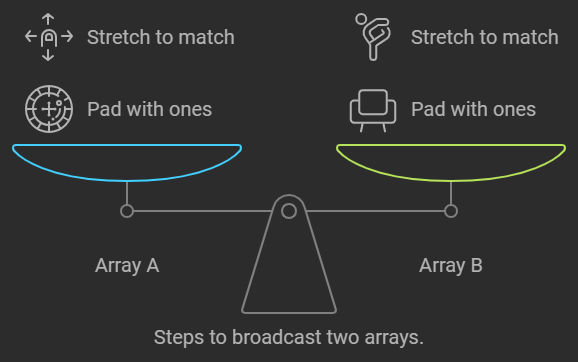
- If two arrays differ in their number of dimensions, the array with fewer dimensions is “padded” with ones on its left side until both arrays have the same number of dimensions.
- For each dimension:
- If the sizes of the two arrays match, that dimension is compatible.
- If one of the arrays has a size of 1 in a particular dimension, the array is “stretched” to match the size of the other array in that dimension.
- If neither of the above conditions is met, the arrays are incompatible, and the operation cannot be broadcasted.
Example of Broadcasting:
python
Copy code
import numpy as np
array_1 = np.array([[1, 2, 3], [4, 5, 6]])
array_2 = np.array([10, 20, 30])
result = array_1 + array_2
print(result)
In this example, array_2 is stretched to match the shape of array_1 so that their elements can be added element-wise. This results in:
lua
Copy code
[[11, 22, 33],
[14, 25, 36]]
Broadcasting in NumPy
Boardcast function similar function is a natural ability of NumPy, one of the most often used numerical computing libraries available in Python. Under the hood, NumPy manages broadcasting so that users may operate on arrays of varying forms free from concern for shape mismatches.
One of the reasons broadcasting is so ubiquitous for jobs involving array manipulation, like scientific computing and machine learning, is how simple it is in NumPy.
Broadcasting in TensorFlow
Popular for deep learning, TensorFlow also uses broadcasting for tensors. Operations involving tensors of various forms—mathematical multiplication or addition—use broadcasting to guarantee compatibility between tensors of different sizes. In neural networks where tensors commonly reflect weights and activations with different forms, this is vital.
Example in TensorFlow:
python
Copy code
import tensorflow as tf
tensor_1 = tf.constant([[1, 2], [3, 4]])
tensor_2 = tf.constant([10, 20])
result = tensor_1 + tensor_2
print(result)
TensorFlow will automatically broadcast tensor_2 to match the shape of tensor_1.
Comparison: Broadcast Function vs. Manual Reshaping
Developers had to physically rearrange arrays to make them compatible before broadcasting was generally embraced. This sometimes included building loops to go over the elements or copying arrays. By removing these procedures, broadcasting simplifies the code.
Manual Reshaping Example:
Without broadcasting, you would need to manually reshape or repeat an array to match another’s shape, like so:
python
Copy code
array_2 = np.array([[10, 20, 30], [10, 20, 30]])
result = array_1 + array_2
While this method works, it increases memory usage and can slow down operations on larger datasets.
Advantages of Using Broadcasting
- Simplicity: Broadcasting makes the code more readable and concise by eliminating the need for manual reshaping.
- Efficiency: Broadcasting optimizes performance, as no actual data is copied or repeated in memory, making it faster and more memory-efficient.
- Flexibility: Broadcasting works seamlessly across different dimensions and shapes, providing flexibility when working with arrays of varying sizes.
Disadvantages and Limitations of Broadcasting
- Incompatibility: If arrays are not compatible for broadcasting, operations will result in errors. Understanding the rules of broadcasting is essential to avoid such pitfalls.
- Confusion: The automatic stretching of arrays can sometimes lead to unexpected results, especially if you’re not fully aware of how broadcasting works under the hood.
Real-World Examples of Broadcasting
In machine learning, batch processing is frequently accomplished using broadcasting. Broadcasting helps you to apply the same transformation to every data point from a batch of points, for instance.
Batch Normalization Example:
In neural networks, normalization of data across a batch can be done efficiently using broadcasting, rather than processing each data point individually.
Common Errors with Broadcasting
Broadcasting suffers regular mistakes when arrays are incompatible for operations. This can occur when the arrays’ dimensions vary in a way that defies broadcasting rules’ applicability.
Example of an Error:
python
Copy code
array_1 = np.array([[1, 2, 3],, [4, 5, 6]])
array_2 = np.array([10, 20])
result = array_1 + array_2 # This will raise a ValueError.
The dimensions of array_2 are incompatible with array_1, leading to an error.
Broadcast Function in PyTorch
Broadcasting is accomplished in PyTorch much like in TensorFlow and NumPy. PyTorch tensors automatically broadcast during operations like matrix addition or multiplication, therefore enabling deep learning models to manage different data shapes.
Broadcast Function in Other Libraries
Other libraries use broadcasting as well; JAX, a rising star for high-performance machine learning, is among them. These libraries guarantee compatibility and performance by letting developers create code that can run on arrays with varied forms.
How Broadcasting Enhances Computational Efficiency
Through avoidance of needless memory allocation, broadcasting increases computational efficiency. Broadcasting allows the reusing of current data structures instead of copying arrays, hence lowering the memory footprint and accelerating processes.
Alternative Functions Similar to Broadcasting
While broadcasting is highly effective, other techniques can also handle arrays of varying shapes:
- Padding: This involves adding zeros or other values to arrays to make them the same size.
- Reshaping: Some libraries allow arrays to be reshaped or flattened so they can be used in operations, though this doesn’t have the same flexibility as broadcasting.
- Tiling: Arrays can be replicated across a dimension to match another array’s size, though this method increases memory usage.
Conclusion
For everyone dealing with arrays, tensors, or matrices, the broadcast capability and related operations are absolutely essential tools. Broadcasting improves code readability, performance, and flexibility by streamlining element-wise operations on arrays of varying forms. Understanding broadcasting can help you avoid hand array manipulation and make your code both faster and more elegant whether your tool is NumPy, TensorFlow, or PyTorch.
FAQs
- What is broadcasting in NumPy?
Broadcasting in NumPy refers to the process of making arrays with different shapes compatible for element-wise operations by stretching smaller arrays. - Can broadcasting lead to errors?
Yes, if the arrays’ dimensions are incompatible, broadcasting will result in a ValueError. - Is broadcasting memory-efficient?
Yes, broadcasting avoids copying data, making it more memory-efficient than other techniques like tiling. - How does TensorFlow handle broadcasting?
TensorFlow automatically broadcasts tensors during operations, following the same rules as NumPy.
What are alternatives to broadcasting?
Alternatives include padding, reshaping, and tiling arrays, though these methods can be less efficient.

