Hey there! Let’s discuss Algebra 1—but not in a mechanical, monotonous manner. Suppose we are simply chatting casually about it. Like a nice study session or a algebra 1 with chit chat over coffee, you know In this sense, algebra will seem more controllable even if it initially seems a bit challenging. All set to leap right in? Let’s leave!
What is Algebra?
In algebra, a subfield of mathematics, we represent numbers using symbols—often letters like x or y. Variables—these symbols—allow us to create expressions and equations reflecting real-world circumstances. If you have three apples and acquire x more, for instance, you now have three plus x apples. Algebra is working here!
Why Is Algebra Important?
Why ought you to give algebra 1 with chit chat some attention? Well, it is everywhere! Algebra helps you think logically, solve issues, and it’s also employed in real-life circumstances like computing budgets, measuring distances, or figuring out how long it will take you to get someplace if you travel at a particular speed. Moreover, if you wish to advance in math—in geometry, calculus, even computer science—understanding algebra is really essential.
Basics of Algebra 1
Understanding Variables
Alright, then variables are only symbols for unidentified numbers. See them as sort of placeholders. Should I say x = 5, you now understand x to be 5. Still, it might be anything until I define x for you. Variables let us address issues where some values are unknown right away.
What Are Expressions and Equations?
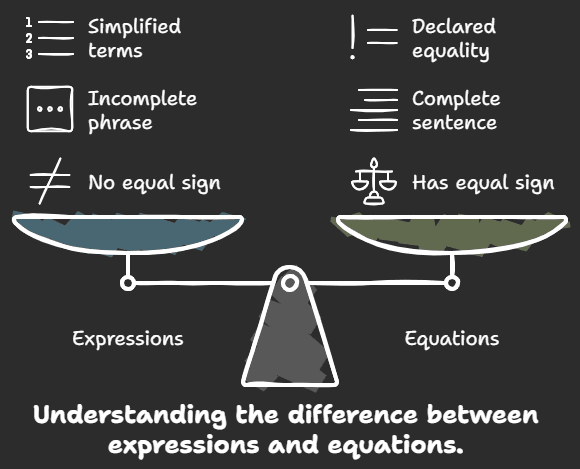
One important one is this. An expression in algebra is a set of numbers, variables, and operations—like addition, subtraction, multiplication, or division. For instance, 3x + 4.
Conversely, an equation is more of a declaration of two things being equal. Three times four, for instance, equals ten. Look at the equal sign? It becomes an equation from that.
Difference Between Expressions and Equations
Equations have an equal sign; expressions lack this. Right, easy enough? Consider it as though an equation is a complete sentence and an expression is only a phrase.
Simplifying Expressions
Simplifying phrases is doing them as straightforwardly as feasible. For two times plus three times, for instance, you can combine the x terms to get five times. You are simply adding like terms, much as when apples are combined with oranges or vice versa.
Solving Equations
One-Step Equations
Let’s begin straightforward. Exactly what it sounds like—a one-step equation—one which you can solve in one step. X plus 5, for instance, equals 10. All you have to do is deduct five from both sides to discover x = five. Simple Peasy!
Two-Step Equations
Let us now turn it up a level using two-step equations. Two times plus three equals eleven, for instance. Subtract 3 from both sides first to find 2x = 8. Divide both sides by 2 next to get x = 4. See. Two steps at most!
Multi-Step Equations
You will come across equations as you go that call for more than two steps to find. Suppose you have 3(x + 2) – 4 = 11. First distribute the 3 to get 3x + 6 – 4 = 11. Stated otherwise, 3x plus 2 equals 11. To find x = 3, subtract 2 from both sides then divide by 3.
Common Mistakes When Solving Equations
Little blunders like failing to distribute or mix terms wrongly are easy. One ploy is to slow down and double-check every action. Trust me; even professionals sometimes make similar mistakes!
Inequalities in Algebra
Understanding Inequalities
Though they have symbols like <, >, ≤, or ≥ rather than an equals sign, inequalities are similar equations. X > 5, for instance, indicates that x is more than 5; nevertheless, it may also be 6, 7, or even 100!
Solving Inequalities
Dealing with inequalities is like working through equations. You handle things on both sides, but be careful! Should you divide or multiply by a negative quantity, you have to reverse the inequality sign. If you are solving -2x > 6, for example, you would divide by -2; but, be sure to flip the sign so x < -3.
Graphing Inequalities
Graph an inequality such as x > 5 by first drawing a number line, marking an open circle at five (because x isn’t equal to five), and shading everything to the right of five. Should the inequality be x ≥ 5, you would fill in the circle to illustrate x might also be 5.
Working with Exponents and Polynomials
Introduction to Exponents
Exponents let one multiply an integer by itself. For instance, 2^3—that is, “2 to the power of 3″—means 2 x 2 x 2, or 8. Particularly with big numbers, exponents speed calculations.
Adding, Subtracting, and Multiplying Polynomials
Polynomial expressions have several terms. A poisson might be 2x^2 + 3x + 5, for instance. You just join like phrases to add or subtract polynials. Multipling them can call for applying the distributive property—more on that soon!
The Distributive Property
A quite useful technique in algebra is the distributive property. It allows you multiply a phrase outside of parenthesis by everything inside. In 3(x + 4), for instance, you would distribute the 3 to get 3x + 12.
Factoring in Algebra 1
What is Factoring?
Factoring is the technique of dissecting an expression into simpler components (factors) whose combined multiplication results in the original statement. You might factor x^2 – 9, for instance, as (x – 3)(x + 3).
Factoring Trinomials
Factoring trinomials like x^2 + 5x + 6 calls for experience. You’re looking for two numbers that multiply to give you the last term (6 in this case) and add up to give you the middle term (5). Here the factors are x + 2)(x + 3).
Conclusion
You thus have it right there. Algebra 1 is not scary. You’ll be calculating equations and handling inequalities like a pro with a little work, patience, and maybe even some chit-chat with friends. Just keep in mind to double-check your work, go step by step, and most importantly—don’t hesitate to make mistakes—that’s how you grow!
FAQs
What is the best way to understand algebra?
Start with the basics and practice regularly. Don’t rush; focus on understanding how and why things work.
Why are variables used in algebra?
Variables represent unknown values and allow us to solve problems with numbers we don’t yet know.
What’s the difference between an expression and an equation?
An expression is a mathematical phrase without an equals sign, while an equation includes an equals sign and shows equality between two sides.
How do you solve multi-step equations?
Break it down into smaller steps: simplify, combine like terms, and perform operations on both sides to isolate the variable.
Why is algebra important in real life?
Algebra helps develop problem-solving skills and is used in many real-life situations, from calculating finances to planning trips.

